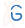Interpret linking data - pair of chromosomes

The user can upload and analyze two types of data: either a single chromosome, or a whole cell. In this section we explain how to identify entanglement between a pair of chromosomes. This analysis can be conducted based on random, centre of mass, or direct closure method. Entanglement of links is also computed by Gaussian linking integral, which is another measure of entanglement between a pair of chromosomes. Moreover, the user can use all these methods together with the relaxation procedure to estimate entanglement stability [1].

Entanglement of a pair of chromosome is presented in the following manner. The information displayed from top to bottom of the result page can be divided into:

Each of these parts is described in detail below. Additional examples are shown here - examples.



Interpreting job status

At the top of the page, the first tab indicates the status of a submitted job. The tab summarizes options used by the user to submit a job and current job performance. All this information is described here



Entanglement of a pair of chromosomes - interactive matrices

Comprehensive information about an entanglement of a pair of chromosomes is presented using three interactive matrices as shown in Fig. 1.

  • Linking of chromosomes - an interactive matrix showing via different colors a type of entanglement determined based on knots polynomials. Color code used to denote given type of the entanglement is presented below matrix. The details about type of an entanglement can be seen upon pointing above the element of the matrix. Off-diagonal element described a topology between a pair of chromosomes - the link type. The symbol U in the topology notation denotes probably unlinked chromosomes. The symbol # in the notation denotes component knots - a sum of prime knots, e.g. 31. Thus 31#31 denotes two 31 knots tighten on a single chromosome. On the diagonal elements described topology of single chain - the knot type. In the case of probabilistic methods the most probably type of entanglement is presented. Details about given type of entanglement are presented in the interactive tables: Knots and Links.
  • Whole Guassian Linking Number - an interactive matrix describing via the intensity of the color winding between the whole chromosome one and the whole chromosome two determined with Gaussian Linking Number approach. The color scale is adapted to address concrete case, however white color always denotes whGLN close to zero - unlinked chromosomes, the most red and dark blue (grey) the highest type of winding in the given case. When whGLN is bigger than 1 there is high probability that the chromosomes are linked.
  • Max |Gaussian Linking Number| - an interactive matrix, which described via the intensity of the color winding between a given chromosome e.g. 1 and any fragment of other chromosome e.g. 2, and a chromosome e.g. 2 and any fragment of a chromosomes e.g. 1. Upon pointing the mouse above given matrix element exact value of Max|GLN| is shown. The color scale is adapted to address concrete case, however, white color always denotes whGLN close to zero - unlinked chromosomes, the most red and dark blue (grey) the highest type of winding in the given case.

Let us remind that Max |GLN| is equal max{maxGLN-minGLN}, where minGLN and maxGLN denote respectively minimum and maximum values of GLN between a chromosome 1 and any fragment of a chromosomes 2, and a chromosome 2 and any fragment of a chromosomes 1.

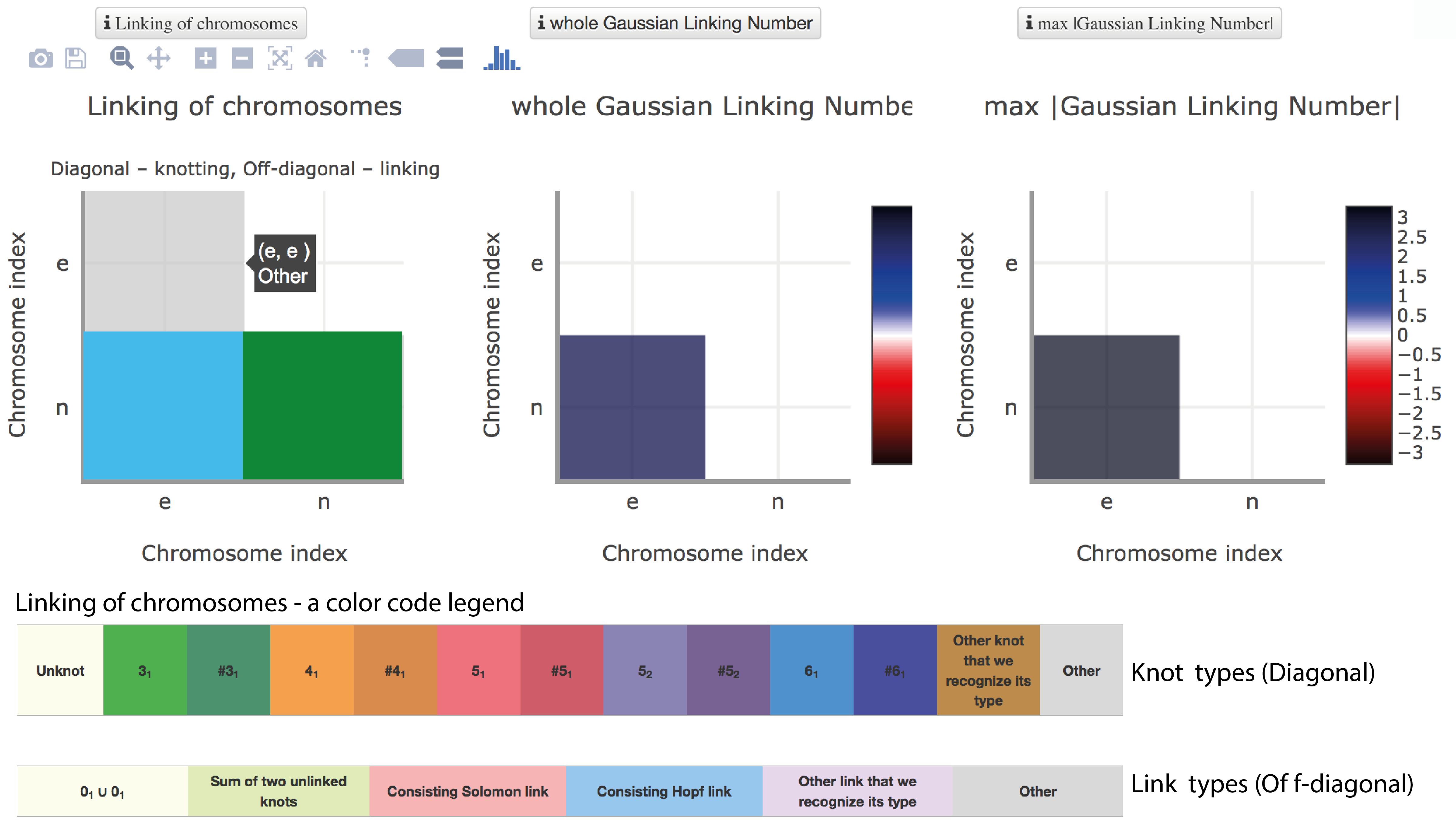
Fig. 1 Overview of a comprehensive analysis of a pair of chromosomes, first part of an example page. Left: the interactive matrix - Linking chromosomes - showing with color code identified knots, links. The color code used in the Knot Gnome is shown below the matrix. Midle and right: interactive matrices to shows entanglement computed based on Gaussian linking integral, which is another measure of entanglement between a pair of chromosomes. The definition of whGLN and max|GLN| is provided here. Upon pointing the cursor on the element of matrix detail information about topology is provided. Upon clicking on the element of matrix a new webpage will be provided containing the Graphical representation of the chromosomes and knot or link likelihood, and the more extended version of the knot or link table is displayed. All matrices can be e.g. zoom in/out, modified and save using open source tool Plotly which allows interactive data visualization (https://plot.ly/).



Table summarizing detected types of knots

The topological and structural details about the knot or the most probable knot (in the case of probabilistic method) are stored in the table below three the matrices (Fig. 1). Each row of the table describes knotting on a single chromosome chain. By default the chromosomes with a trivial topology are not shown in the table, they are listed in the table by clicking the button "Toggle hidden" above the table. In each row, one can find the miniature depiction of the identified knot along with its name and probability. Upon clicking on View details - located in the left-most part of the table - a new website is provided which contains the Graphical representation of the chromosomes, knot likelihood, and the knot table. This content is the same as in the case of the Main type knot analysis and is described here. When probabilistic method is used, this table contains other types of knots identified for this chromosome not presented in the main page.

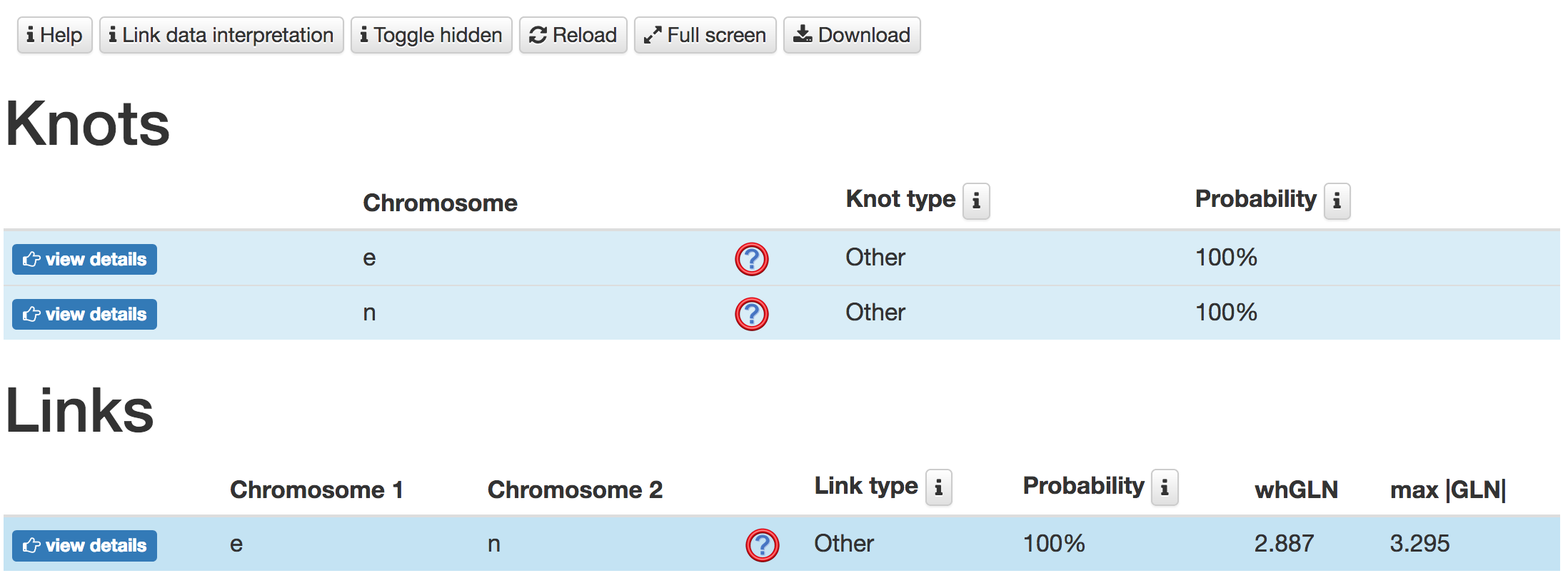
Fig. 2 Tables showing indentified knots and link in analyzed exemplary pair of chromosomes. Tables contains the types entanglement, schematic drawing of topology, probability and entanglement measured with Gaussian Linking Number - whGLN, max|GLN|. Upon clicking on "view details" a new webpage including the Graphical representation of the chromosomes and the knot or link likelihood, and the more extended version of the knot or link table will appear. Presented data were analyzed with the centre of mass method. Above the tables are places additional buttons to facilitated further analysis. The button "Toggle hidden" should be use to include in the tables trivial topologies. The download button allows downloading all topological information about the investigated structures presented in the tables, to perform own analysis.



The topological and structural details about the most probable type of link are stored in the table (Fig. 2), below the matrices (Fig. 1). Each row of the table (when only one pair is analyzed table contains one row) describes linking between a pair of chromosomes. In each row, one can find the miniature depiction of the link identified along with its name and probability, values of whGLN and max|GLN|. Upon pointing the cursor on max|GLN| the user can see the range of atoms corresponding to the shortest fragments of the chromosomes which wind around each other (for details see GLN description). Upon clicking on View details - located in the left-most part of the table - a new website is provided with the graphical presentation of chromosomes and link likelihood, and the link table. This subpage is described here. Composition of these information on the one website allows user to verified (e.g. results of closure method) and understand better topological analysis. When the random closure method is used this table contains also other types of identified links - not only the most probability link.

Graphical representation of chromosomes and link likelihood

Details about indentified links are presented on subpage which contains the JSmol presentation of the chromosomes structures (left) and the pie chart (right) representing the likelihood of each link identified. By default the most probable link type is show in the center of the pie chart.

  • Chromosomes structures are presented using JSmol applet as shown in Fig. 3. Chromosome fragments colored in cyan and magenta indicate the shortest fragments with the highest value of max|GLN| (the most right numbers in the table bellow graphical representation). Remaining fragments are colored by different intensities of gray. When the direct closure method or the centre of mass method was used the result of closure - geometry - is directly visual on the chromosomes. The orange strip between the first and last atom show closure when the direct closure method is used. Two straight lines connected by an arc lying on the surface of the sphere represent closure of the single chromosome when the centre of mass method is used. This option allows e.g. identification of closure that introduces an artificial link. Graphical closure can be turn on and off. The structures are visualized based on The JSmol applet which comes with standard JSmol options, i.e. the user can rotate and zoom the structure, or change its colors, representation etc. In particular, the user can display only one chromoseme by right-clicking on the picture, and selecting All models→1.1, or change color by right-clicking on the picture, and selecting Color→Atoms→Green. Moreover, the vizualization can be downloaded as a e.g. png file.
  • Link Likelihood pie chart. The pie chart presents all indentified links - Fig. 4. The center of the plot depends on the position of the cursor. Placing the cursor on some part of the chart changes its content to the scheme of the corresponding link with its likelihood given in percentage. By default, the most probable link is shown in the center of the plot. When deterministic methods are used the link likelihood shows one detected type of link, the left pie chart in the Fig 4. The presentation of the link likelihood via pie chart comes from [1].

Fig. 3 An example of chromosomes structures presentation using JSmol applet when the deterministic method is used. These chromosomes are unlinked, however, each single chromosome forms a 31 knot.

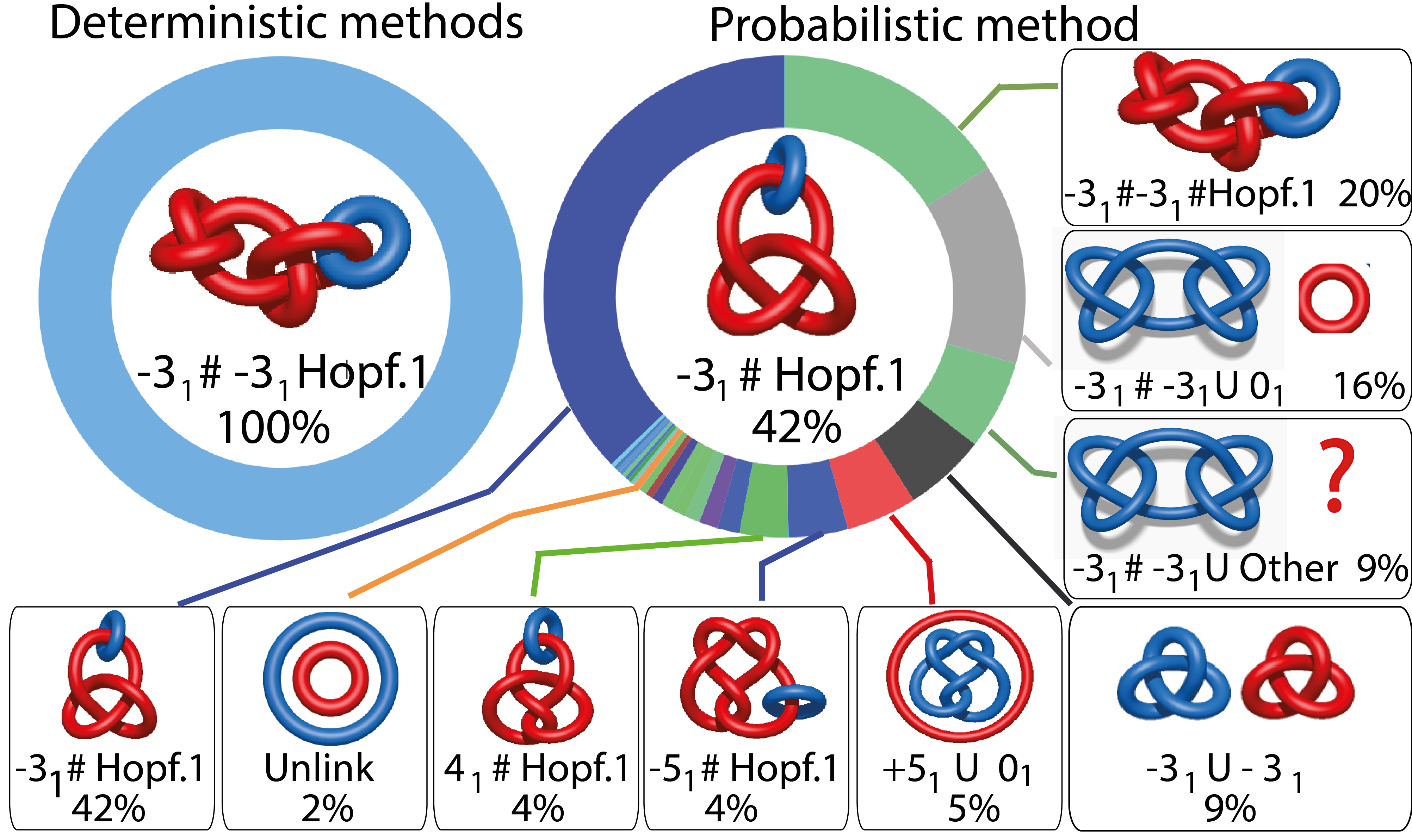
Fig. 4 The pie chart representing the likelihood of the links identified. Left, an example of a pie chart when the deterministic closure methods are used. Right, an example of a pie chart when random closure method is used. In the case of random closure method by default, the most probable link is shown in the center of the plot. Upon placing the cursor over a region of the chart, the corresponding link and its likelihood are displayed in the center of the pie chart.



Examples

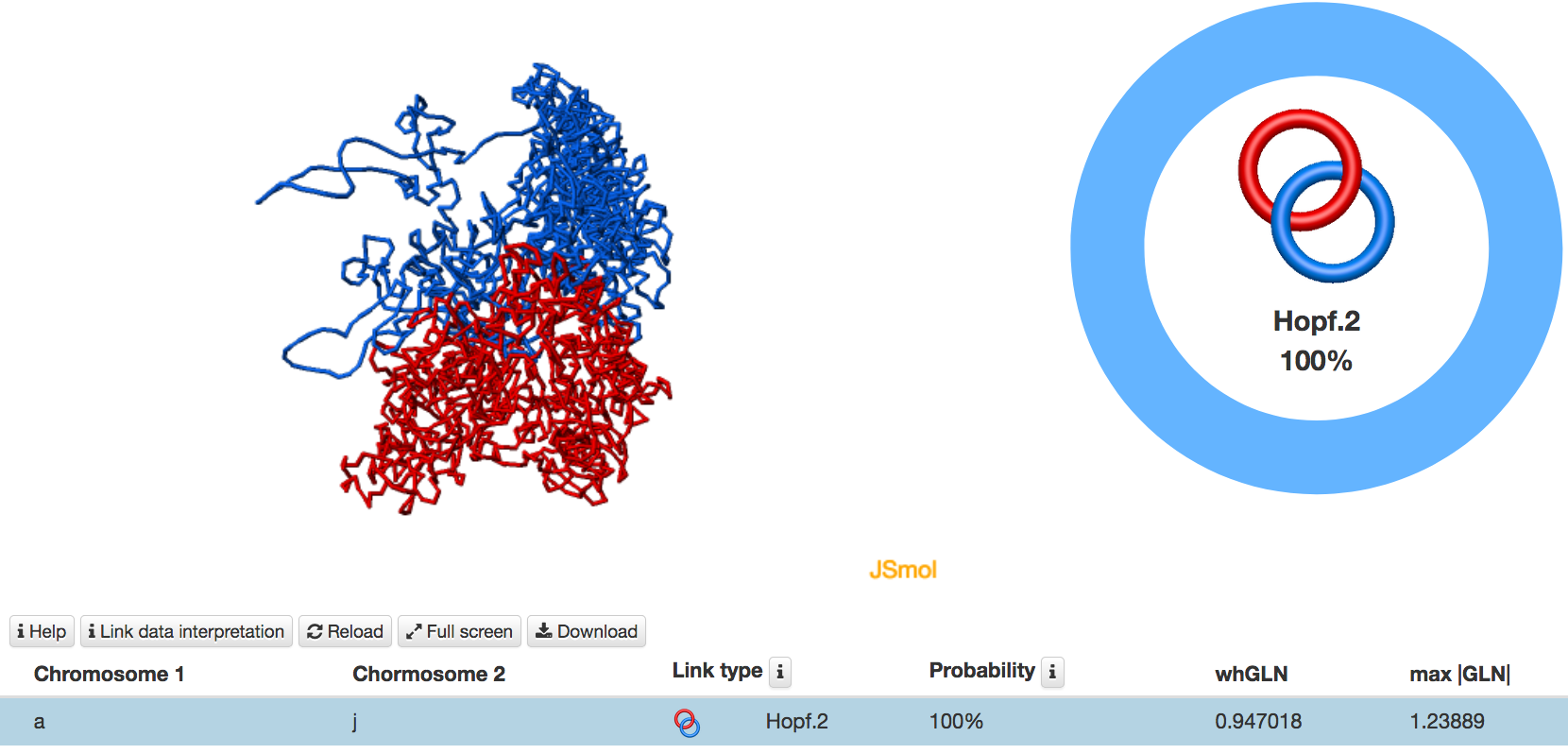
Fig. 5 Example of analysis of a pair of chromosome structures based on deterministic method. These chromosomes form a Hopf.2 link.

Fig. 6 Example of analysis of a pair of chromosome structures based on deterministic method. These chromosomes form a 4_1#Hopf.2 link.

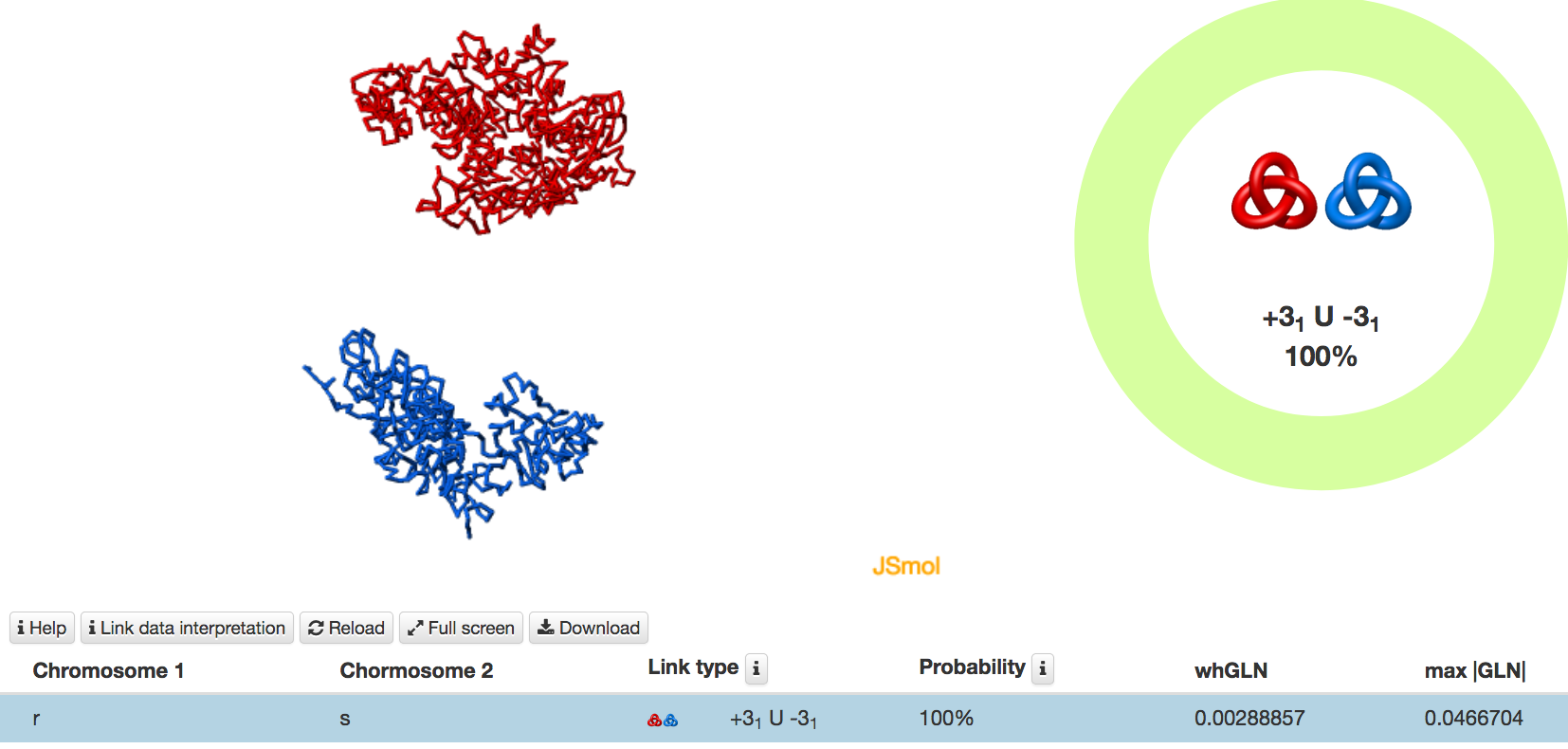
Fig. 7 An example of analysis of a pair of chromosome structures based on deterministic method. These chromosomes are unlinked, however each single chromosome forms a 31 knot.



[1] Dabrowski-Tumanski P*, Jarmolinska AI*, Niemyska W*, Rawdon E, Millett K, Sulkowska JI, LinkProt: database collecting information about biological links, Nucleic Acids Res. (2016) doi: 10.1093/nar/gkw976
How to cite
KnotGenom | Interdisciplinary Laboratory of Biological Systems Modelling