Introduction
KnotGenom detects two types of links, probabilistic and deterministic, depending on the method used to close chromosomes termini [1]. For more details about closure methods see section "Link detection". Next, the collections of links of n components are separated according to the number of crossings that appear in a generic orthogonal projection of the given link to a two dimensional plane with the smallest number of crossings. The classification of links is unique (for more details see http://linkprot.cent.uw.edu.pl/link_detection). Within each subcollection, individual links are ordered according to historical practice, e.g. the Alexander-Briggs table, or, in more contemporary listings, according to a facet of their symbolic coding, e.g. the Dowker-Thistlethwaite code with the 'alphabetical' ordering.
For each n component link, there may be as many as 2n+1 oriented links varying by mirror reflection (and the chirality of the link) and the orientation of the individual components. The result is that the identification of an m crossing n-component link quickly becomes a very challenging problem. In practice, there is a small series of steps that one can take to achieve this identification:
- First one applies mathematical algorithms to simplify the spatial position of the realization of the n component link so as to give a generic orthogonal projection that has a few crossings. Note, that one has to make sure that these simplifications do not change the topological type of the link.
- One next codes the oriented link using, for example, the Dowker-Thistlethwaite code, and applies mathematical algorithms that simplify the DT code by further reducing the number of coded crossings. Note, that these simplifications do not change the topological type of the link.
- One next calculates a knot polynomial, in our case the HOMFLY-PT polynomial, and consults a table to establish the relationship between the polynomial and the associated n component link. If it is in the table, either there is a unique corresponding link and, if not, one undertakes further topological analysis using other invariants quantities to identify the link.
If a link is divided into k spatially separated families of sublinks, we determine the identity of the sublinks, Li, and show the entire link as the union of these sublinks, e.g. using these strategies, namely Dabrowski-Tumanski et al. in [1], we developed a table of link polynomials for those that have occurred in proteins the most frequently. As new ones are encountered, we use these methods to identify them and add them to tables if this is possible. However, as it is shown below by the examples, links detected between chromosomes are much more complex.
The majority of above description comes from http://linkprot.cent.uw.edu.pl/link_detection where more details can be found.
Links detection
Links are detected between chromosomes upon joining the termini of each chromosome. To detect links, the KontGenome uses a modified technique developed before for multichain models of proteins [1]. The method is optimized here to take into account properties of chromosomes as described below.
The server provides three options:
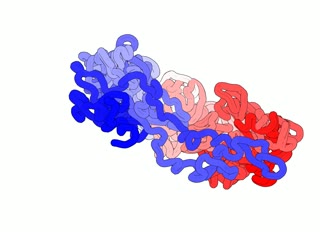
- Random closure method (Fig. 1A). The termini are expanded towards one point the large sphere randomly. In general, type of the link depends on the direction of expansion. Therefore, an option of 10 closures is used as default one, however, the user can change this value. Such links are also called probabilistic. The probability of each link is given as a percentage (%). This method is the most time consuming but it gives the highest probability that detected links are not artificial.
- The centre of mass method (Fig 1B). Each chromosome endpoints are connected to two points on the sphere based on directions determined by their positions and the centre of mass. These two points are connected by an arc lying on the surface of the sphere. The results of this method has to be carefully evaluated - please see Fig. 1B.
- Direct closure method (Fig 1C). Each chromosome endpoints are connected by the shortest interval.
Fig. 1 Methods used in KnotGenom to connect chromosome endpoints. Panel A — random closure method. Panel B — the centre of mass method. Panel C — direct closure method.
Remark 1: Please notice that each of these methods can introduce an additional crossing of the chain in its projection on 2D plane, changing artificially its link type. Therefore, the random closure method is recommended to use, however, this is the most time consuming method.
Remark 2: To speed up calculation and to avoid artificial links as shown in Fig. 1, before calculating a link invariants additional condition is checked. This condition estimates probability that two chromosomes could form a link. If any bead from the chromosome 1 is further than 5Å from the chromosome 2 or vice versa, we assume that these two chromosomes are not linked. In such situation we do not determine a link (we assume that chromosomes are unlinked) and we determine knots along each of these chromosomes separately. This approach allows us also to classify a bigger number of links.
Links classification
The KnotGenom uses three closure methods to determine links (for details see Links detection). In each category, the links are divided into topological classes and by the number of components which constitute the link. Each topological class is then subdivided into more exact subclasses taking into account also the chirality of the link. The topological classification of each link type is described in this section following nomenclature which we established before for linked proteins. Currently, the KnotGenom server presents information about links made of:
When the probabilistic method is used, the link type in principle depends on the closure direction. In such case the link type is calculated for many closure directions (default values is equal 10) and the total likelihood variation of the associated topological link types is presented for each pair of chromosomes. Moreover, the user has the possibility to define the cut-off likelihood for which the structures will be displayed. With decreasing the likelihood cut-off, more structures and more topological motifs are present. The default likelihood cut-off is set at 30%.
For the center of mass and the direct closure method, the probabilities are denoted as 100% as there is only one closure in these cases.
The KnotGenom server also takes the orientation of the chains into account, which splits the possible topological type into subtypes. Currently, the HOMFLY-PT polynomial is used to identify all prime two-component links up to 14 crossings in their minimal crossing representation and most component links up to 8 crossings [1]. However, some knots and links observed in current chromosomes conformation [3] contain even more crossings. Such type of entanglement is called "Other". Such structures reflect chains that form exceptionally complicated links or knots, and they will be progressively identified and added to the database. Examples of probabilistic links identified in chromosomes are presented in Table 1.
Remark 1: Other - denotes links or knots with more than 8 crossings.
Remark 2: U in the name of a link denotes unlinked chromosomes, where at least one chain possesses a non-trivial topology. For example 31 U unknot denotes an unlinked pair of chromosomes, where one chromosome possesses a 31 knot and the second one is unknotted.
Remark 3: # in the name of a link denotes composite knots, which are knot sums of a few prime knots. For instance 31 # 41 denotes a knot made of two trefoil knots on a single chromosome. Thus 31 # 41 U unknot describes an unlinked pair of chromosomes, where one chromosome possesses a composite knot and the second one is unkotted; and 31 # 31 # 2.1 describes linked chromosomes, one possesses composite knot and the second one forms a ring.

Fig. 2 Examples of the notation for unlinked chromosomes. Left panel: 31 U unknot, middle panel: 31 # 41 U unknot, right panel: 31 # 21.
Two-component links - please see link classification for more details.
Two-component unlinks.
[1] Dabrowski-Tumanski P*, Jarmolinska AI*, Niemyska W*, Rawdon E, Millett K, Sulkowska JI, LinkProt: database collecting information about biological links, Nucleic Acids Res. (2016) doi: 10.1093/nar/gkw976
[2] Dabrowski-Tumanski P, Sulkowska JI, Topological knots and links in proteins, PNAS (2017) doi: 10.1073/pnas.1615862114
[3] Millett KC, Rawdon EJ, Stasiak A, Sulkowska JI, Identifying knots in proteins Biochemical Society Transactions (2013) 41(2):533-7, doi: 10.1042/BST20120339